Modélisation hydraulique avec RANS : Principes et définitions
La modélisation hydraulique RANS[1] repose sur la méthode des volumes finis. Cette méthode s’appuie sur un maillage pour mener à bien ses simulations. Le domaine que l’on souhaite simuler est coupé en un certain nombre de mailles, de formes diverses (en 3D généralement des tétraèdres ou des pavés, des pyramides pour les audacieux mais sérieusement, n’utilisez pas ces dernières…). Chacune des mailles est connecté à ses voisines par ses faces.
L’ensemble de la simulation consiste à calculer pour chaque maille quels sont les flux qui traversent les faces pour en déduire ce qu’il se passe au sein de la maille et ce, à chaque itération. En simulation dite steady (i.e. permanente), on répète le processus sur autant d’itérations que nécessaire pour atteindre la convergence. La convergence est un état d’équilibre à partir duquel la simulation n’évolue plus. Chaque nouvelle itération fournit peu ou proue la même solution que l’itération précédente.
Les limites de la modélisation avec RANS
L’un des défauts de cette méthode, c’est que les résultats de la simulation sont parfois impactés par le maillage lui-même. La forme et la tailles des mailles utilisées ont une influence significative sur les résultats des calculs de la modélisation hydraulique. Le pavé par exemple est une maille qui a une direction privilégiée. À moins d’utiliser des cubes, le pavé aura une longueur, une largeur et une hauteur toutes différentes, avec généralement une longueur supérieure au deux autres qui seront sensiblement les mêmes. Si le flux de ce que vous cherchez à simuler n’est pas majoritairement dirigé dans le même sens que votre plus grande longueur de maille, les résultats de simulation auront plus de difficultés à coller à la réalité.
En hydraulique, l’écoulement a généralement un sens privilégié. L’eau s’écoule dans un sens, il y a peu de chances qu’une partie de l’eau décide de remonter à contre-courant. C’est la raison pour laquelle il nous est possible d’utiliser les pavés comme maille. Mais pour toutes les simulations en aéraulique ou en transfert isotropique [3] (par exemple de chaleur), le pavé est une maille à proscrire et les tétraèdres lui seront généralement préférés. Un maillage composé uniquement de tétraèdre est très chaotique et ne privilégie aucune direction particulière, permettant de laisser l’isotropie de ce que vous modélisez s’exprimer.
RANS vs PIXELS
De la même manière, le nombre de maille utilisé va définir la résolution et la justesse avec laquelle vous allez pouvoir obtenir vos résultats de modélisation hydraulique. On pourrait faire une analogie avec un personnage de jeux vidéo. Sur la figure ci-dessous, vous pouvez 3 modèles différents du même personnage très connu de la série des Tomb Raider. Sur la gauche, il s’agit du modèle utilisé pour Tomb Raider 1. Le nombre de polygone (subdivision faisant partie d’un modèle dans un jeux vidéo, équivalent des mailles pour une simulation RANS) qui sert à représenter Lara Croft est très limité, elle n’a pas de doigts ou d’orteils marqués, pas de coude ou de poignet et ses cheveux sont une masse unique. Le modèle du centre est celui de Tomb Raider 4, qui possède déjà plus de polygone, nous permettant de deviner des épaules, des poignets, des coudes ou de mieux marquer ses genoux. Elle n’a cependant toujours pas d’orteils et ses cheveux restent une masse unique, un peu plus détaillée que pour le modèle précédent. Enfin, à droite, une version bien plus récente, bien plus détaillée, que ce soit au niveau des cheveux, des orteils ou de ses accessoires.
Cette analogie vous donne une première idée de l’influence du maillage sur les résultats de simulations.
Revenons à la physique
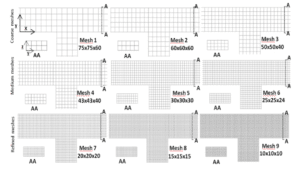
Regardons maintenant concrètement comment cela se traduit pour une modélisation hydraulique avec RANS .La figure suivante montre plusieurs maillages pour la même géométrie : une jonction.
Nous avons 9 maillages différents, du plus grossier (mailles de 7,5 cm par 7,5 cm par 6 cm) correspond au modèle de Tomb Raider 1 jusqu’au plus fin (mailles de 1cm de côté), correspond au modèle le plus récent de Lara Croft.
Les champs de vitesses obtenus après convergence pour les maillages 1, 5 et 8 sont montrés ci-après. Les résultats sont centrés sur le champ de vitesses après la jonction, pour deux élévations différentes (3 cm à gauche et 9 cm à droite).
On remarque que les champs de vitesses pour les 3 maillages sont différents, alors que c’est la même situation qui est modélisée dans les 3 cas. L’évolution est plus subtile entre le maillage 5 et le maillage 8 mais encore notable. Ces changements dans les résultats de simulation indiquent que les résultats obtenus avec les maillages 1 et 5 ne sont pas indépendants du maillage utilisé.
Pour prouver que le maillage 8 est suffisamment fin pour ne pas influencer les résultats, il faut que les champs de vitesses donnés par les simulations utilisant le maillage 9 soient les mêmes. L’indépendance des résultats au maillage est toujours liée à la variable que l’on souhaite utiliser. Dans cet exemple, il s’agit du champ de vitesse. Si ça avait été la forme de la surface libre (le champ des hauteurs d’eau dans la jonction), on aurait pu voir que dès le maillage 3, les résultats de simulation sont indépendants du maillage.
Pour aller plus loin
Ci-après, d’autres exemples tirés de publication scientifiques qui font les choses bien en démontrant que la variable qui les intéresse est bien indépendante du maillage.
Evolution des coefficients de portance (en haut) ou de trainée (en bas) avec le nombre de mailles. Les résultats sont indépendants du maillage pour les modèles à 8 millions de mailles et plus (Extrait de JEONG, Kiyeon, JUNG, Eunhee, KANG, Dong-Gi, et al. Grid Dependency and Aerodynamic Analysis for Transonic Flow of Delta Wing using CFD. Journal of the Korean Society for Aeronautical & Space Sciences, 2018, vol. 46, no 6, p. 445-451).
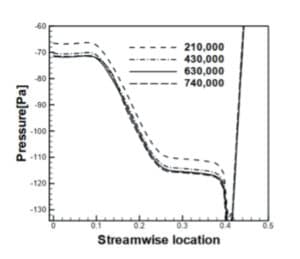
Evolution de la pression en fonction de la position, dans le sens du courant. Les résultats de simulation sont indépendants du maillage pour les modèles à 630 000 mailles et plus. Extrait de LEE, Ki-Sang, KIM, Kwang-Yong, et SAMAD, Abdus. Design optimization of low-speed axial flow fan blade with three-dimensional RANS analysis. Journal of mechanical science and technology, 2008, vol. 22, no 10, p. 1864-1869.
Lorsqu’on utilise la modélisation hydraulique 3D RANS à des fins de métrologie pour des ouvrages spéciaux du réseau d’assainissement, comme les déversoirs d’orage, il est primordial de démontrer que les résultats de la simulation sont indépendants du maillage. Cette preuve ne peut que prendre la forme de résultats de simulation obtenus pour un maillage plus dense que celui qui permet d’établir la position du capteur et la loi de transformation hauteur-débit.
Si cette preuve n’est pas donnée, vous n’avez aucune garantie que les résultats de simulation représentent la réalité plutôt que l’impact du maillage sur le système d’équation que RANS cherche à résoudre. En particulier, lorsque l’on souhaite déterminer l’emplacement d’un capteur de hauteur d’eau de sorte à ce que la hauteur d’eau mesurée puisse nous permettre de suivre le débit déversé, il est indispensable de démontrer l’indépendance du maillage pour les hauteurs d’eau, le champ de vitesse et les débits.
C’est l’une des raisons qui nous a poussé, chez ÆGIR, à partir sur une méthode de modélisation hydraulique SPH, qui n’utilise pas de maillage. Dans SPH, le fluide modélisé est remplacé par des particules, dont la taille définit directement la résolution du calcul. Il suffit de choisir une taille de particule de l’ordre du plus faible niveau de résolution pertinent pour le calcul (généralement autour de l’incertitude du capteur de mesure, soit environ 1cm) pour obtenir une simulation représentant la réalité fidèlement.
[1] Reynold-Averaged Navier-Stokes
[2] Momplot, A., Bonakdari, H., Mignot, E., Lipeme Kouyi, G., Rivière, N., & Bertrand-Krajewski, J. L. (2012, September). Effects of computational meshes on hydrodynamics of an open channel junction flow using CFD technique. In Proceedings of the 9th International Conference on Urban Drainage Modelling. Belgrade, Serbia.
[3] Qui se diffuse de manière égale dans toutes les directions

 [2]
[2]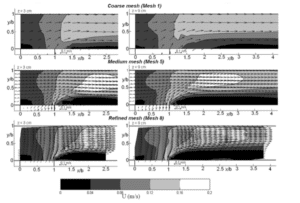 [2]
[2]
0 commentaires